Stelling van Pythagoras deel 5 meerdere stappen berekenen wiskunde tv YouTube

Online Pythagoras calculator. Maak eerst een keuze welke driehoek je gaat gebruiken. Geef de hoekpunten en lengten van 2 zijden op. Klik daarna op "Berekenen". Je krijgt dan de uitwerking met de Stelling van Pythagoras. Handig als naslagwerk bij opgaven uit je boek! Laat steeds 1 van de 3 zijden leeg! Bereken online de zijden in een.
Stelling van pythagoras lange zijde berekenen YouTube

De stelling van Pythagoras deel 4: Een zijde berekenen m.b.v. een Pythagoreïsch drietal. De stelling van Pythagoras speelt een enorm belangrijke rol in de oude architectuur, bijvoorbeeld bij de bouw van piramides. Ook bijvoorbeeld de Indiërs de Babyloniërs gebruikten de stelling om een rechte hoek te maken bij de constructie van grote.
Stelling van Pythagoras Hoe werkt het? DEES Amsterdam

Deel II Goniometrie en precalculus 2. Wiskunde In zicht een cursus wiskunde voor studierichtingen met component wiskunde derde graad algemeen secundair onderwijs geschreven door. Koen De Naeghel.
Bereken De Rechte Zijde Met De Stelling Van Pythagoras

De stelling van Pythagoras.. c is de zijde tegenover de rechte hoek. a en b zijn de andere twee. Voorbeeld 1. Bereken het vraagteken in de figuur hiernaast Oplossing: x 2 = 4 2 + 5 2 = 16 + 25 = 41 Dus x. Bereken de oppervlakte van 8 e driehoek in deze serie.
Wanneer En Waarvoor Gebruik Je De Stelling Van Pythagoras?
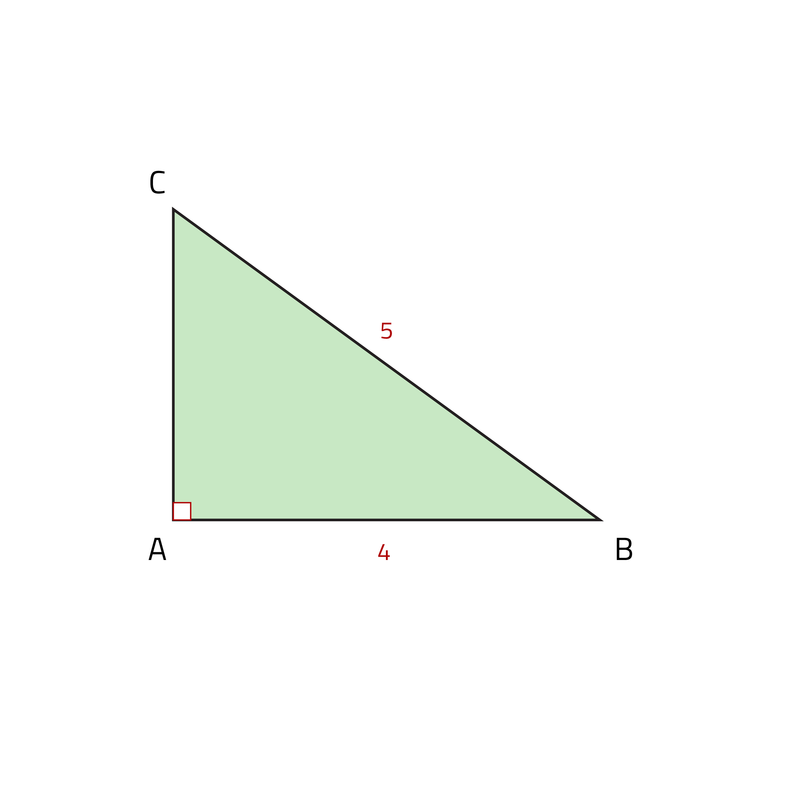
De stelling van Pythagoras is a 2 + b 2 = c 2. Als je de lengte van twee zijdes hebt, blijft er dan nog een onbekende die je kunt uitrekenen via deze formule. De a en b in de formule zijn de zijde die aan de rechte hoek zitten. De c is de schuine zijde van de driehoek. Dit is ook te zien in figuur 1. Figuur 1: Driehoek met een loodrechte hoek.
De stelling van Pythagoras StudyGo
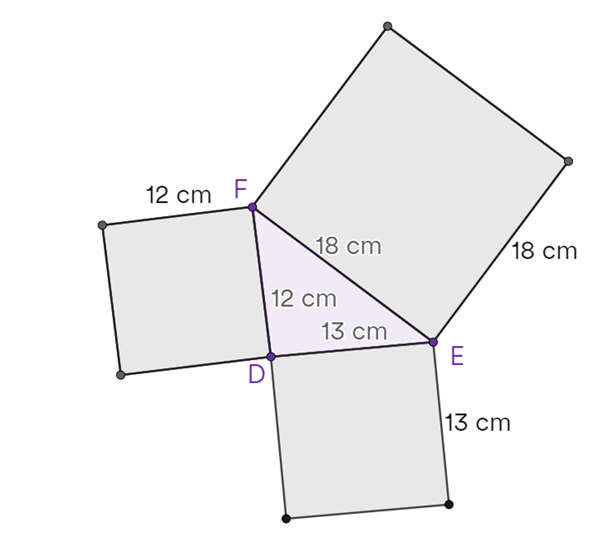
Ga naar http://www.WiskundeAcademie.nl/onderwerpen/Pythagoras voor nog meer gratis uitlegvideo's over toepassingen van de stelling van Pythagoras of bekijk d.
PPT Toepassingen op de stelling van Pythagoras PowerPoint Presentation ID489727
Voorbeeld van de stelling van Pythagoras. Sal gebruikt de stelling van Pythagoras om de hoogte te berekenen van een een rechthoekige driehoek met basis 9 en schuine zijde 14. Gemaakt door Sal Khan en Monterey Institute for Technology and Education.
Stelling van Pythagoras II YouTube

De stelling van Pythagoras. Een rechthoekige driehoek heeft 3 zijdes: 2 rechthoekszijden en een schuine zijde. De schuine zijde wordt ook wel eens de langste zijde, of de hypotenusa genoemd. Bij de stelling van Pythagoras kan je de schuine zijde berekenen wanneer je de 2 rechthoekszijden weet. De stelling wordt vaak aangegeven als a 2 + b 2 = c 2.
Stelling van Pythagoras Deel 2 De langste zijde berekenen (2 VMBOK) YouTube

Dit is een rechte hoek. de basislijn gaat van links naar rechts, de rechterzijde recht omhoog, dus een rechte hoek. Dus als we van deze zijden de lengte weten kunnen we de stelling van Pythagoras gebruiken om de lange zijde te berekenen, de zijde tegenover de recht hoek dat is de hypotenusa dat is de hypotenusa Ik schrijf dat op. De afstand is.
Stelling van Pythagoras deel 4 bereken de rechthoekszijde wiskunde tv YouTube

In deze video leer ik je hoe je een langste zijde van een rechthoekige driehoek kunt berekenen met de stelling van Pythagoras.
Digistudies Hoeken berekenen Wiskunde uitleg vmbo
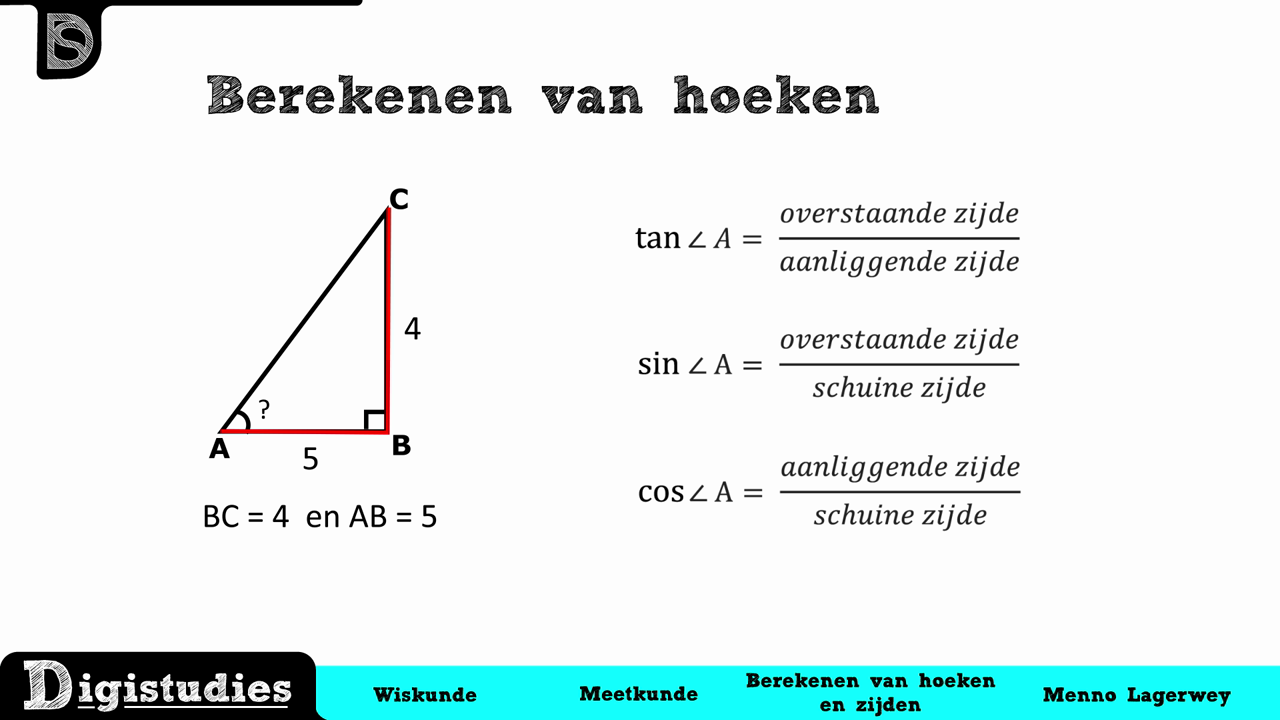
Om de werking van de stelling van Pythagoras nog verder te verduidelijken, staat hieronder een voorbeeld weergegeven. Dit voorbeeld kan gebruikt worden voor alle verschillende getallen. Als voorbeeld zeggen we dat de lengten A = 4 en B = 5. De schuine lengte noemen we C. Stap 1: 4 2 + 5 2 = 16 + 25 = 41. (De lengte van C moet worden berekend.
Stelling van Pythagoras. Bereken de omtrek. GeoGebra
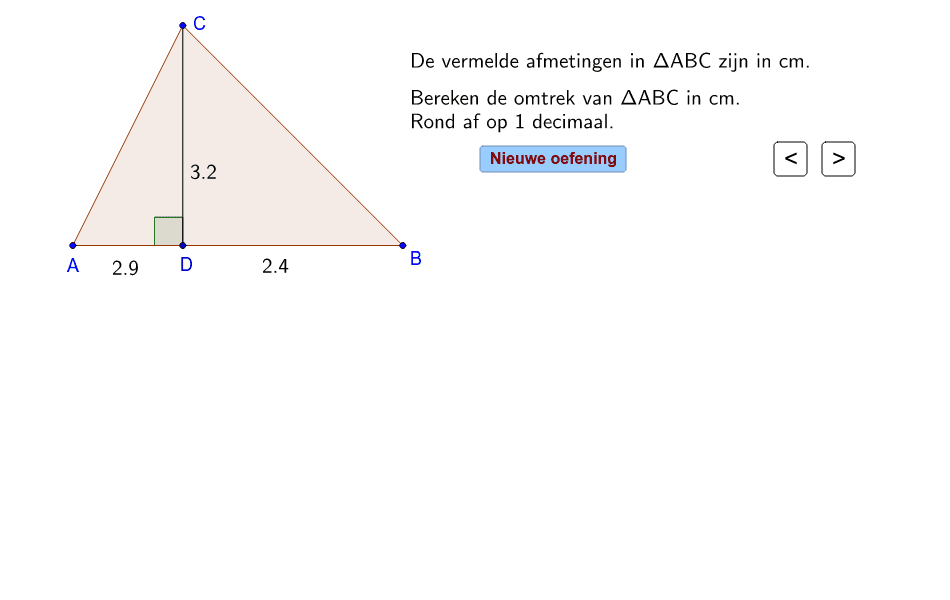
Omdat we hier nu drie driehoeken hebben. We hebben driehoek ADC, driehoek DBC, en we hebben de originele grotere driehoek. En hopelijk kunnen we gelijkvormigheid bepalen tussen deze driehoeken. Eerst zal ik je laten zien dat ADC gelijkvormig is aan de grotere. Omdat beiden een rechte hoek hebben.
Stelling van Pythagoras en bekende driehoeken YouTube

In deze video leer je de rechthoekszijde van een rechthoekige driehoek te berekenen, wanneer je de andere twee weet.
Stelling van pythagoras korte zijde berekenen YouTube

De lengte van een zijde in een rechthoekige driehoek berekenen met de stelling van Pythagoras. Thiago vraagt: hoe snel moet een keeper reageren op een strafschop? Wiskunde > Beginselen algebra >. Dit is de rechte hoek, deze zijde noem ik a en heeft lengte 21. en deze zijde hier heeft lengte 35. Misschien zeg je nu 35 kwadraat plus 21.
Korte zijde berekenen (Pythagoras) YouTube
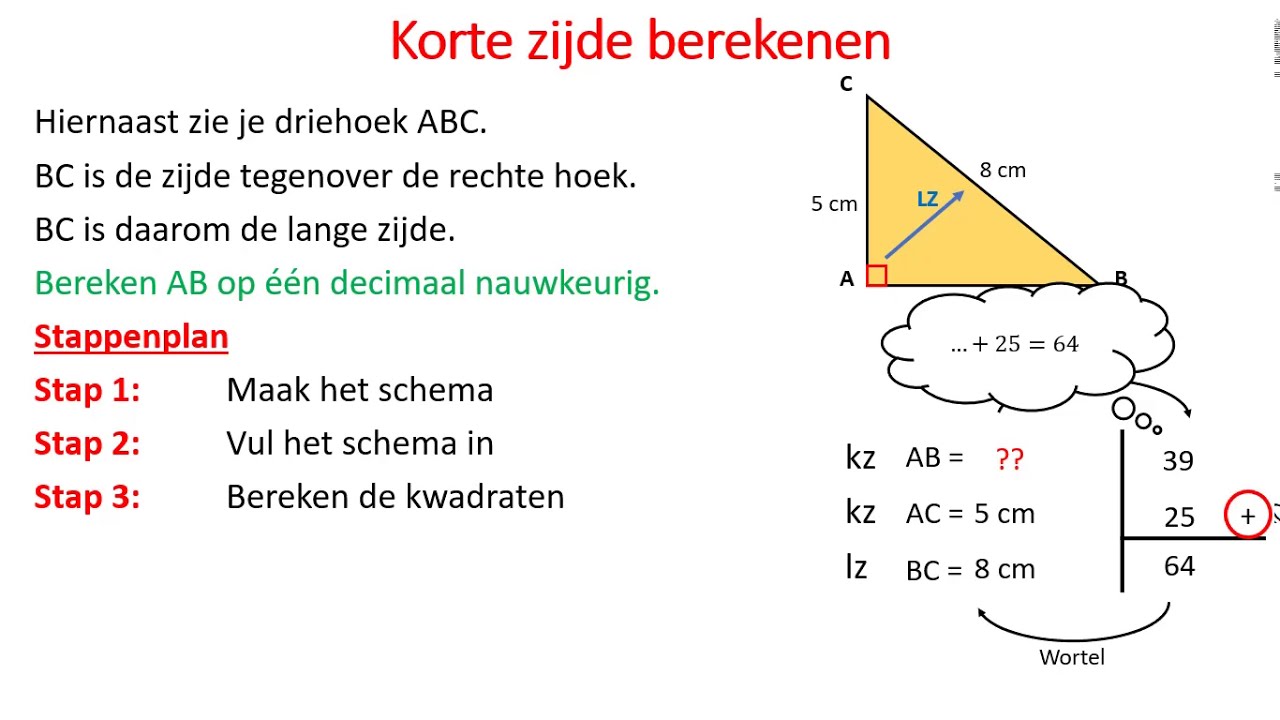
Je kunt de Stelling van Pythagoras toepassen in rechthoekige driehoeken. Stelling van Pythagoras: (ene rechthoekszijde) 2 + (andere rechthoekszijde) 2 = (schuine zijde) 2. Of ook wel bekend als: a2 + b2 = c2, waarbij a en b de rechthoekszijden zijn en c de schuine zijde is. Om de afstand van een lijnstuk in een assenstelsel te berekenen, kun je.
Oefening stelling van Pythagoras GeoGebra
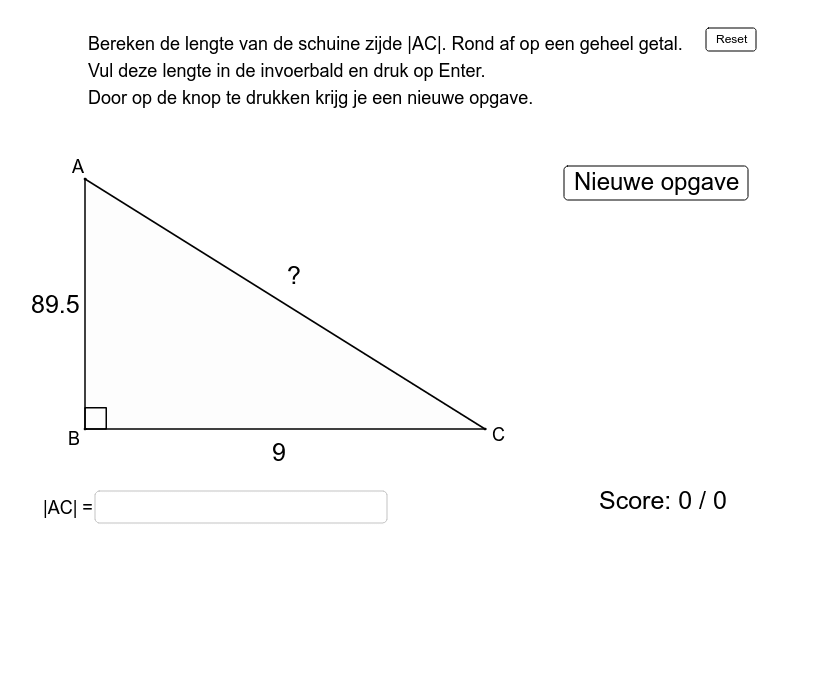
De stelling van Pythagoras is een van de bekendste wiskunde formules. De stelling luidt: de som van het kwadraat van de lengtes van de rechthoekszijden is gelijk aan het kwadraat van de lengte van de schuine zijde. Kortom: A 2 + B 2 = C 2 Hierbij is A de lengte van de korte zijde, B de lengte van de lange zijde en C de lengte van de schuine zijde.